Salam sejahtra bagi kita semua, kali ini kami memposting materi persamaan diferesial biasa. Jadi, silahkan anda membuat kopi, panggil teman anda dan beli cemilang setelah itu berdiskusilah, jangan gibah wkwkwk...
PERSAMAAN DIFERENSIAL BIASA
Persamaan Diferensial Biasa (ordinary differential equation) disingkat
PDB adalah suatu persamaan diferensial yang hanya mempunyai satu variabel
bebas. Jika y(x) adalah suatu fungsi satu variabel, maka x dinamakan variabel
bebas dan y dinamakan variabel tak bebas. Persamaan (1), (2), (3) adalah contoh
PDB.
Orde persamaan diferensial ditentukan oleh turunan tertinggi dalam
persamaan tersebut, contoh:
Persamaan di atas dapat ditulis dg notasi lain yaitu:
Derajat (degree) dari suatu persamaan diferensial adalah pangkat
tertinggi dari turunan tertinggi suatu persamaan diferensial, contoh:
Syarat tambahan pada persamaan diferensial, untuk satu nilai variabel
bebas yang mempunyai satu atau lebih nilai syarat disebut syarat awal (initial
conditions). PD dengan syarat awal dikatakan sebagai suatu masalah nilai awal
(initial-value problem). Jika syarat yang diberikan pada PD lebih dari satu
nilai variabel bebas, disebut syarat batas dan merupakan PD dengan masalah
nilai batas (boundary-value problem).
Solusi (Penyelesaian) PDB
Beberapa jenis
solusi PD akan dijabarkan sebagai berikut:
Solusi PD bentuk
eksplisit yaitu solusi PD dengan fungsi yang mana variabel bebas dan variabel
tak bebas dapat dibedakan dengan jelas. Solusi eksplisit dinyatakan dalam
bentuk y = f(x). Contoh solusi/fungsi eksplisit:
Solusi PD bentuki
implisit yaitu solusi PD dengan fungsi yang mana variabel bebas dengan variabel
tak bebas tidak dapat dibedakan secara jelas. Fungsi implisit ditulis dalam
bentuk f(x,y) = 0. Contoh solusi/fungsi implisit:
Penyelesaian implisit
dan penyelesaian eksplisit, keduanya secara singkat biasa disebut penyelesaian
PDB. Solusi Persamaan Diferensial Biasa (PDB) terbagi dalam tiga jenis solusi
yaitu:
·
Solusi
Umum (Penyelesaian Umum): solusi PDB yang masih mengandung konstanta sebarang
misalnya c.
·
Solusi
Khusus/Partikulir (Penyelesaian Khusus/Partikulir): solusi yang tidak
mengandung konstanta variabel karena terdapat syarat awal pada suatu PDB.
·
Solusi
Singular (Penyelesaian Singular): solusi yang tidak diperoleh dari hasil
mensubstitusikan suatu nilai konstanta pada solusi umumnya.
Contoh: diketahui sebagai solusi
umum dari PDB:
diketahui sebagai solusi
umum dari PDB: tetapi disisi lain PDB
tersebut mempunyai penyelesaian lain:
tetapi disisi lain PDB
tersebut mempunyai penyelesaian lain:  ,penyelesaian ini
disebut sebagai penyelesaian singular.
,penyelesaian ini
disebut sebagai penyelesaian singular.
 diketahui sebagai solusi
umum dari PDB:
diketahui sebagai solusi
umum dari PDB: tetapi disisi lain PDB
tersebut mempunyai penyelesaian lain:
tetapi disisi lain PDB
tersebut mempunyai penyelesaian lain:  ,penyelesaian ini
disebut sebagai penyelesaian singular.
,penyelesaian ini
disebut sebagai penyelesaian singular.
Metode Penyelesaian. Metode yang digunakan
untuk mencari solusi (menyelesaikan) Persamaan Diferensial antara lain:
1. Metode Analitik: Metoda ini menghasilkan dua
bentuk solusi yaitu bentuk eksplisit dan implisit. Untuk masalah-masalah yang
komplek metode analitik ini jarang digunakan karena memerlukan analisis yang
cukup rumit.
2. Metode Kualitatif: Solusi PDB didapatkan
dengan perkiraan pada pengamatan pola medan gradien. Metode ini memberikan
gambaran secara geometris dari solusi PDB. Metode ini meskipun dapat memberikan
pemahaman kelakuan solusi suatu PDB namun fungsi asli dari solusinya tidak
diketahui dan metode ini tidak digunakan untuk kasus yang komplek.
3. Metode Numerik. Solusi yang diperoleh dari
metode ini adalah solusi hampiran (solusi pendekatan/aproksimasi). Dengan
bantuan program komputer, metode ini dapat menyelesaikan PDB dari tingkat
sederhana sampai pada masalah yang komplek.
Ketiga metode tersebut dapat diselesaikan dengan software MATLAB.
Ketiga metode tersebut dapat diselesaikan dengan software MATLAB.
Pembentukan Persamaan Diferensial
Secara matematis, persamaan diferensial muncul jika ada
konstanta sembarang dieliminasikan dari suatu fungsi tertentu yang diberikan.
Contoh: Bentuklah persamaan diferensial dari fungsi berikut
Penyelesaian:
dari fungsi yang diberikan (soal) konstanta
sembarang A adalah:
sehingga
sehingga
Satu contoh lagi, bentuklah persamaan
diferensial untuk
Penyelesaian:
substitusikan konstanta A ke:
sehingga
dengan mensubstitusikan A dan B pada
persamaan:
kita dapatkan:
Hasil akhir penyelesaian di atas adalah
persamaan diferensial orde dua. Jadi fungsi dengan satu konstanta sembarang
menghasilkan persamaan diferensial orde satu, sedangkan fungsi dengan dua
konstanta sembarang menghasilkan persamaan diferensial orde dua. Sehingga
berlaku kaidah:
Fungsi yang mempunyai n buah konstanta
sembarang akan menghasilkan Persamaan Diferensial orde ke-n
Sedikit tambahan :(
Contoh Soal:
Bentuklah persamaan diferensial dari
 didapat
didapat



Cukup saja materi ini sampai disini tapi bohoong....
Beberapa hari kedepan, kami akan memberikan materi kelanjutannya
Tetap dirumah saja
Jaga kesehatan
dan yang suka rebahan disinilah skill lo diuji :)
Contoh Soal:
Bentuklah persamaan diferensial dari

Turunkan kedua ruas terhapa x, diperoleh
Subtitusikan A ini ke didapat
didapat


Jadi persamaan
diferesialnya adalah
1. Carilah
persamaan diferensial dari himpunan garis lengkung y = Ce-4x dan C
adalah konstanta sembarang
Ingatlah rumus turunan fungsi
transenden berikut, dengan u menyatakan fungsi dalam variabel
bebas x.
Karena ada satu konstanta sembarang,
maka dibutuhkan 2 persamaan untuk mengeliminasinya dan orde
tertinggi dari turunannya adalah 1.
Persamaan 1:
Persamaan 1:
Turunkan terhadap x, diperoleh
Tentukan persamaan diferensial dari x = y – (y2 + 1)
1. Tentukan penyelesaian umum dari 2y” – 8 = 0
Misalkan
y adalah fungsi dari x, sehingga
1. Bentuklah persamaan diferensial dari y = A Sin x + B Cos x
Ingat bahwa
turunkan
sekali lagi terhadap x, diperoleh
Dengan
demikian, kita dapatkan
Cukup saja materi ini sampai disini tapi bohoong....
Beberapa hari kedepan, kami akan memberikan materi kelanjutannya
Tetap dirumah saja
Jaga kesehatan
dan yang suka rebahan disinilah skill lo diuji :)





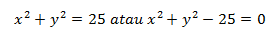






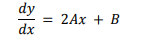


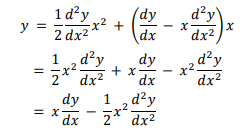








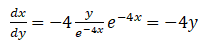






Komentar
Posting Komentar