Hai sobat Mad School, maaf nih baru sempat posting karena harus dipahami dulu baru dipost :(. kali ini kami memposting materi Turunan dan Integral. So, cekidot....
TURUNAN DAN INTEGRAL
TURUNAN
Turunan Matematika adalah pengukuran terhadap
Fungsi yang berubah seiring perubahan Nilai Inputnya karena secara umum Turunan
Matematika itu menyatakan bagaimana suatu besaran dapat berubah akibat
perubahan besaran lainnya. Sebagai Contoh, Turunan dari Posisi sebuah benda
yang bergerak terhadap waktu ialah Kecepatan yang sesaat dari Objek tersebut
dan proses dlm menemukan Turunan disebut dengan Diferensiasi.
- (in x)’
- (sin x)’ = cos x
- (cos x)’ = -sin x
- (tan x) = sec2 x
- y’ merupakan simbol untuk turunan pertama.
- y” merupakan simbol untuk turunan kedua.
- y”’ merupakan simbol untuk turunan ketiga.
A.
TURUNAN PERTAMA
Misalnya
y merupakan fungsi dari x atau dapat ditulis juga y=f(x). Turunan dari y
terhadap x dinotasikan sebagai berikut:

Dengan
menngunakan definisi turunan diatas dapat diturunkan beberapa rumus-rumus
turunan, yaitu :
Perhatikan contoh
berikut :
Perhatikan contoh
berikut :
Perhatikan contoh
berikut :
4. Untuk y=f(x).g(x)
maka
atau dapat juga kita
misalkan f(x)=u dan g(x)=v sehingga rumus turunan u.v=u’v+uv’
B.
TURUNAN KEDUA
Turunan kedua dari
y=f(x) terhadap x dinotasikan sebagai berikut
Turunan kedua merupakan
turunan yang diperoleh dengan menurunkan kembali turunan pertama. Perhatikan
contoh berikut :
INTEGRAL
Integral
secara sederhana dapat disebut sebagai invers (kebalikan) dari operasi turunan. Kita sebut F suatu anti turunan dari f pada selang I
jika DF = f pada I – yakni, jika F’(x) = f(x) untuk semua x dalam I (jika x di
suatu titik ujung dari I, F’(x) hanya perlu berupa turunan satu sisi)
A.
Notasi Integral
Apabila fungsi F(x) sebuah anti turunan dari fungsi
f(x) maka dapat dituliskan
∫ f(x) dx = F(x) + C
Dan dibaca “integral dari sebuah fungsi f(x) terhadap
x adalah fungsi F(x) tambah konstanta C.”
Keterangan mengenai notasi integral:
·
Simbol ∫ adalah simbol integral yang menunjukan banyak bentuk umum anti
turun fungsi f(x). Simbol ini diperkenalkan oleh Leibniz seperti huruf “S”
dari kata “sum” yang berarti penjumlahan.
·
f(x) sesudah simbol ∫ dinamakan fungsi integral
·
Simbol dx setelah fungsi integral f(x) untuk menunjukan diferensial
terhadap x (setelah huruf d dari dx), adalah variabel integral.
·
F(x) dinamakan fungsi primitif atau fungsi dari integral dari f(x)
·
C dinamakan konstanta integral
Contoh integral:
Dalam soal ini, batas
atas adalah 1 dan batas bawah -2. Tahap pertama yang perlu kita lakukan adalah
melakukan integral fungsi 3x2 + 5x + 2
menjadi seperti di bawah ini.
Setelah kita mendapatkan bentuk integral dari fungsi
tersebut, kita dapat memasukkan nilai batas atas dan bawah ke dalam fungsi
tersebut lalu mengurangkannya menjadi seperti berikut.
Hasil dari integral tersebut adalah 27,5.
Sifat
Integral
Beberapa
sifat integral yaitu sebagai berikut.

B. Integral Tak Tentu
Seperti yang telah dijelaskan pada
bagian sebelumnya, integral tak tentu merupakan suatu kebalikan dari turunan.
Kalian dapat menyebutnya sebagai anti turunan atau antiderivative.
Integral tak tentu dari suatu fungsi
menghasilkan fungsi baru yang belum memiliki nilai yang tentu karena masih
terdapat variabel dalam fungsi baru tersebut. Bentuk umum integral tentu .
.
Keterangan:
 .
.
Rumus:
Keterangan:
f(x) : persamaan kurva
F(x) : luasan di bawah kurva f(x)
C : konstanta
Contoh integral tak
tentu:
C. Integral Tentu
Integral tentu didefinisikan sebagai jumlahan suatu
daerah yang dibatasi kurva atau persamaan tertentu. Berbeda dari integral tak tentu, integral tentu
memiliki nilai tertentu karena batas yang ditentukan sudah jelas.
Secara umum, integral tentu didefinisikan sebagai
Keterangan:
f(x) : persamaan kurva
a, b : batas bawah dan batas atas integral
F(b), F(a) : nilai integral untuk x = b dan x = a.
Contoh integral
tentu:
Carilah hasil
dari ʃ21 6x2 dx !
Jadi, hasil dari ʃ21 6x2 dx adalah
14.
D. Integral Substitusi
Beberapa permasalahan atau integral suatu fungsi dapat
diselesaikan dengan integral substitusi jika terdapat perkalian fungsi dengan
salah satu fungsi merupakan turunan fungsi yang lain.
Perhatikan contoh
berikut.
Kita misalkan U = ½ x2 + 3 maka dU/dx = x
Sehingga x dx = dU
= -2 cos U + C = -2
cos ( ½ x2 + 3) + C
Contoh Subtitusi:
E.
Integral Parsial
Integral parsial biasa digunakan untuk
menyelesaikan integral dari perkalian dua fungsi. Secara umum, integral parsial
didefinikan dengan
Keterangan:
U, V : fungsi
dU, dV : turunan dari fungsi U dan turunan dari fungsi
V
Contoh Integral Parsial:
Tentukan
hasil dari ʃ (2x+1) cos (x + π) dx !
Misal
dv = cos (x
+ π) dx
Maka
du = 2 dx
v = ʃ cos (x
+ π) dx = sin (x + π)
Sehingga
∫ u dv = uv
− ∫v du
∫ u dv =
(2x+1) . sin (x +π) − 2 (− cos (x + π)) + C
∫ u dv =
(2x+1) . sin (x +π) + 2 cos (x + π) + C
Jadi, hasil
dari ʃ (2x+1) cos (x + π) dx adalah (2x+1) . sin (x +π) + 2 cos (x + π) +
C.
Maaf ya, mungkin itu sedikit penjelasan kami. inssyallah kami perbaruhi postingan ini biar materinya mudah dipaham... Jika ada saran atau kekurangan pada materi ini tolong dikomen....
Oke !
adapun contoh soal yang kami sediakan, semoga bisa bermanfaat
Contoh Soal
Maaf ya, mungkin itu sedikit penjelasan kami. inssyallah kami perbaruhi postingan ini biar materinya mudah dipaham... Jika ada saran atau kekurangan pada materi ini tolong dikomen....
Oke !
adapun contoh soal yang kami sediakan, semoga bisa bermanfaat
Contoh Soal




















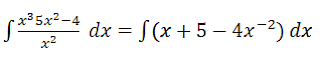



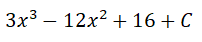

Komentar
Posting Komentar