Tutorial Penyajian Data Menggunakan Microsft Office Excel

Assalamualaikum warahmatullahi wabarakatu...

          Selamat datang di blog Mad Schooling, kali ini kami akan berbagai Tutorial penyajian data menggunakan Microsoft Office Excel

          Pertama tama pastikan  anda punya laptop dan yang terpenting wajib sediakan cemilang dan minuman jasjus, terserah rasa apa :) . Lanjut aktifkan fitur Data Analysis di Excel anda, jika belum silahkan ikuti cara tahap-tahapnya dibawah ini

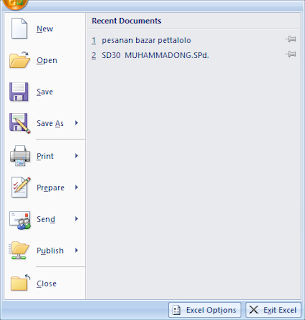
1. Pertama masuk ke menu Office Button yang berada dipojok kiri atas dan pilih option pada bagian bawah



2. masuk ke bagian Add-ins yang berada di sebelah kanan
   


3. pilih Go kemudian centang semua pilihan yang ada untuk mengaktifkan semua fiturnya dan pilih OK
   
   

Tunggu beberapa menit untuk proses pengaktifan fitur Data Analysis. Jika sudah aktif, Sekarang kita bisa menggunakannya , saya akan memberi contoh data seperti digambar bawah ini

Pertama-tama menu Data pada menu bar dan pilih Data Analysis kemudian pilih Histogram lalu klik OK.

Setelah mengklik OK, selanjutnya pada bagian Input Range seleksi semua angka yang ada pada bagian kolom Mantan Pacar (Umur) dan Bin Range seleksi semua rentang kelas yang berada di bagian sebelah kanannya, kemudian pilih Output Range, dan tentukan posisi sel yang diinginkan pada bagian kanan Output Range, maka akan terlihat seperti ini

Pilih OK, maka hasil inilah hasilnya

Bagaimana? Mudahkan?, atau anda ingin menggunakan Diagram Batang
Caranya adalah:

1. Blok semua nilai pada kolom Frequency, pilih menu Insert lalu klik Column maka akan muncul beberapa jenis Column  dan silahkan pilih model sesuai selera anda. setelah itu akan muncul tabel seperti gambar dibawah ini dan jangan lupa beri warna sesuai selera anda sesuai dengan kegantengan dan kecantikan anda :(
   
   
   
   
2. Kita edit angka angka (1,2,3,4,5) menjadi rentang kelas dengan cara, klik kanan, pilih Select Data, setelah itu edit lalu Seleksi rentang kelas dan klik OK sebanyak dua kali.
   
   
   

And Finaly, press buttom CTR+S in keyword dan jadilah Diagram Batang, mungkin hanya itu bisa kami berikan pada pembahasan kali ini, silahkan anda belajar Auto Didac karena saya juga belajar Auto Didac atau perbanyak nonton tutorial dan satu lagi dishare linknya, kasian yang punya blok ngak ada pulsanya takutnya nanti mama minta pulsa :(

sekian dan sampai jumpa lagi beberapa bulan kemudian :)